
For this year’s April A-Z Challenge I am blogging a series of sketches about the free people formerly enslaved on the Cleage plantations in Athens, Tennessee. Most are not related to me by blood, although our families came off of the same plantations – those of Samuel, Alexander and David Cleage. Click on any image to enlarge.
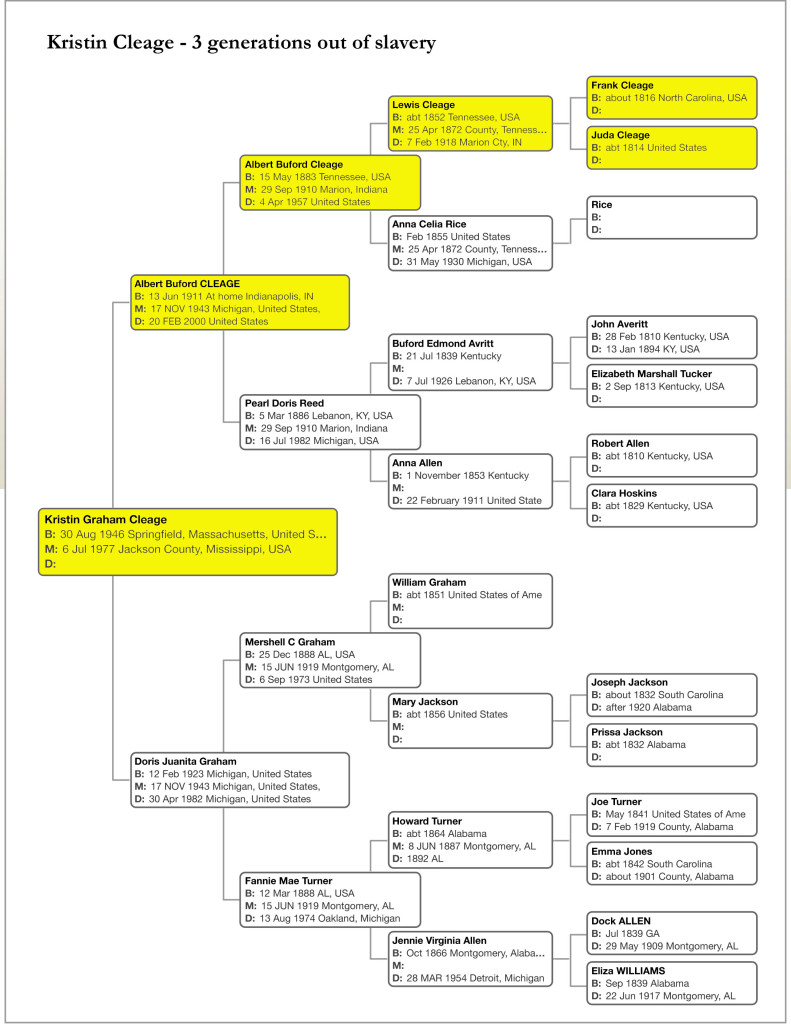
This post is about my relationship to the Cleages of Athens, Tennessee. Kristin Cleage (that is me) was born free in Springfield, Mass. in 1946. My only sister was born when I was 2. My family moved back to Detroit when I was four. I finished high school and graduated with a degree in fine arts from Wayne State University. I worked as a pre-school teacher, a doll maker and a librarian. Eventually I married James Williams, who had an Associates Degree and worked as an organizer and an inspector of asphalt for the Michigan Dept of Transportation. We had six children. All of our children attended college, lived to be adults and most now have children of their own. At various times we have shared our home with children and grandchildren, and other relatives. We owned a variety of homes over the years, some with and some free from mortgage. We often lived around extended family. I was the third generation of my Cleages born out of slavery.
My father, Rev. Albert B. Cleage Jr (aka Jaramogi Abebe Agyeman) was born free in Indianapolis, Indiana in 1911 to parents born in Tennessee and Kentucky. His family moved to Kalamazoo, Michigan and eventually Detroit. He had six siblings. All of them lived to be at least eighty years old. He attended public schools in Detroit and graduated with a BA from Wayne State University, followed by a Divinity Degree at Oberlin College and doing post degree work in film at the University of Southern California. He married my mother, Doris Graham and they had two daughters. Both daughters lived to be adults, graduated from college and had seven children between them. My father pastored churches in Lexington, KY; San Francisco, CA; Springfield, MA and Detroit, MI. He was active in politics and with friends and family, published newsletter, advocated self determination and black power for black people. He founded the Shrines of the Black Madonna with churches in Detroit, Atlanta and Houston. He died at the age of 88 in 2000 in South Carolina. He was the second generation born out of slavery.
My grandfather, Dr. Albert B. Cleage Sr, was born free in Hackberry, Loudon County, Tennessee in 1883. He was the youngest of five children born to Louis Cleage and Celia Rice. Eventually the family moved back to Athens, Tennessee and his parents were divorced. He and his siblings all graduated from high school. Several attended college. My grandfather graduated from Knoxville College in Knoxville, TN and the University of Indiana medical school, Indianapolis, IN. He married my grandmother, Pearl Reed and they had seven children who all lived to age 80 or beyond. After completing his internship, the family moved to Kalamazoo, MI. There he set up his medical practice. After several years they moved to Detroit, Michigan where he opened Cleage Clinic and practiced medicine. Three of his siblings and his mother eventually moved to Detroit. One brother remained in Athens. My grandfather regularly traveled back to visit. During his life, my grandfather helped found three churches and two black hospitals. This was in the days when black doctors could not practice in most white hospitals. In the 1950s my grandfather retired and in 1957 he died in Detroit. He was the first generation born out of slavery.
My greatgrandfather Louis Cleage was born into slavery on Alexander Cleage’s plantation in McMinn County, about 1852. He was fourteen when freedom came with the end of the Civil War. He married Celia Rice in 1872 in Athens, TN and they had five children. They all lived to adulthood and attended high school and/or college. He worked as a farmer, in the steel mills, on the railroad and did other hard labor all of his life. He never learned to read or write. He died in 1918 in Indianapolis, Indiana at his daughter’s home. He lived free for 52 of his 66 years.
My 2X great grandfather Frank Cleage was born into slavery about 1816 in North Carolina. I do not know how he came to be on Samuel Cleage’s plantation, but he was there by 1834 when he was mentioned in the letter to the overseer. My 2X great grandmother Juda Cleage, was born into slavery about 1814. She came to Alexander Cleage’s plantation with his wife, Jemima Hurst. Juda was mentioned in both Elijah Hurst’s and Alexander Cleage’s Wills. Frank and Juda both gained their freedom after the Civil War and were legally married that same year. They had at least eight children. Frank worked as a laborer. I have not found them after the 1870 census. I can only trace three of their children so I am unable to give death ages. The three children I have found all did hard physical labor and were unable to read and write, as were Frank and Juda.

You can read more about each person by following the links or putting a name in the search box in the right hand column.




Love this post, Kristin! I am so enjoying reading your A-Z challenge.
Thanks Andrea! I thought I had so much research already done, and I do, but there’s always something else I want to find as I start writing them up. This one, I knew it all.
What a beautiful, gifted post Kris! As always, you’re doing the CLEAGE Ancestors proud!:)
Thank you Luckie! next year I’ll have to do the Turners and/or the Grahams.
Well Kristin, it’s nice to officially meet you! 😉
Man I wish I knew this much about my family. The information is out there, I just have to bug my relatives to get it.
I love that first picture at the top. Your dad looks so serious, your mom look so happy and your grandfather looks like he might have that mischievous old man streak in him. And of course you’re cute, too. 😉
Get that info while they are here to give it to you! My dad has what we call the “Cleage Look” here. My grandfather died when I was 7 so I didn’t get to spend a lot of time with him. I’m sure he had a dry or biting humor, depending on the occasion. He was 5 years younger than I am now in this photo. Never realized that before. My mother does look happy. I especially like my dirty feet. I only wore shoes when absolutely necessary. I still do that.
Yes, it is vital to get the info while it is available. For example, my father interviewed my grandfather about his WWII experiences and taped the interviews. This is now a treasured family resource, and I learned things from it that I’d never known, not only about my grandfather’s war history, but about my grandfather’s personality. He never used his particular brand of dry wit around us kids, but – it is definitely there in the tapes!
This beautiful post makes me cry, Kristin. Just wanted to thank you for it. Thank you for bearing witness and for inspiring others to do the same. Like the commenters above, I love the pictures of the younger you. And the panoramic photo of your extended family.
It’s always a surprise to me when a post is really affects readers. I used that panoramic view as a header and that is why it won’t blow up too big. I like it too. We had another gathering a few years later and forgot to get a group photo. I regret that.
I am the third generation born free. Three of my four sets of great grandparents were born into slavery. The fourth set barely missed slavery, born in the 1860s after the Civil War.
1 of my great grandmother’s was born free, all the rest were born into slavery. She was born in 1866, but her parents had been freed before the Civil War.
Beautiful post Kristin! I’m loving these series of post you’ve written on the Cleage’s. Also what software did you use to create your lovely chart?
I saved my pedigree on ancestry.com in print mode, opened it in photoshop and added the yellow to highlight the Cleage line.
You could do it with most genealogy software.
I’m really glad you’re enjoying it.
Awesome work!!………..I am sharing all of it with my sister Susan and Ernie
Thank you Greg and thanks for sharing it with Susan and Ernie because I know they do not do online.
great work and presentation!!
gem!
Thanks Gem!
I’m so glad you could include yourself in this A-Z. You have so much information about your family. I can trace our family back to the early 1800s but have no personal information other than their names, dob etc.
It’s fascinating to see the detail you have turned up.
Amazing what I come up with from the records I can find.
It is nice to find out more about you too! 🙂 You have done an incredible amount of research on this, and uncovered some great stories 🙂
@TarkabarkaHolgy from
Multicolored Diary – Epics from A to Z
MopDog – 26 Ways to Die in Medieval Hungary
I can’t believe we aren’t even half way through the alphabet yet!
Your ancestors are amazing. They worked so hard and obviously knew the value of education. And you also seem to have good genes for long life. I really enjoyed learning about this.
I do seem to have long life genes. I’ve got to get it together so I can enjoy the next 20 years!
I’m struck by how much your baby picture looks like the older you. Same laugh!
I just noticed that, same face 22 years later 🙂
This is a wonderful post, Kristin! I often reflect on the fact that I, too, am only the third generation born free in my family. It’s really amazing, isn’t it? I only wish I’d known at least my grandfather, so that I could have heard some stories about his formerly-enslaved parents. But, alas, he died in 1929 – just a bit befor my time (smile), and when father was only 4 years old; so even he didn’t have any memory of him, or stories to tell.
Thanks for the inspiration. I believe I will copy this idea (eventually), and get something posted on Into the LIGHT! 🙂
Renate
I never heard from my grandparents about their parents or grandparents slavery experiences. My mother and my aunts and uncles remembered bits and pieces.
You have inspired me to learn more about my family. How interesting!
Do it! It’s very interesting.
Wow, Kristin! This continues to be amazing! What a resource you are making, for historians as well as for your family and the other Cleage families from the same plantation! And your grandfather was a really handsome man! At least, I think so.
I think so too, Melanie.
I am jumping around and am glad I read this one for context! Great project.
I’m glad you enjoyed it!
You have done excellent research. Very good. In one of your photo packages you have small photo of my Uncle John, my Grandmother Minnie’s youngest. Uncle John was a talented musician; however, he had a sad life. E-Mail me and I’ll write you about it. Read your comments about you and your sister riding bikes west on Tireman avenue to Dearborn. I lived on Tireman from 1940 to 1959. From September 1952 through June 1954 (7th and 8th grade) I attended St. Luke’s grade school located on the corner of Tireman and Ohio street. Going west on Tireman at Ohio street the right side was Detroit and the left side was Dearborn. On good weather days I would ride my speed bike; on the bad weather days I would take the “Tireman Through” bus. At that time the Mayor of Dearborn was Orville Hubbard. Look up his history as Dearborn’s mayor.